
|
Book: Commentary.
The Theoretical Background of Insights.
|
On the Relation of Data Mining and Knowledge Mining
Comments on "Self-Organising Data Mining" by Prof. J.-A. Mueller and F. Lemke
Author of the GMDH self-organizing modeling technology and
Corresponding member of the Academy of Sciences of the Ukraine, Kiev
|
First of all, I must thank the authors for the fact that they dedicated the book to me. I understand this as an acknowledgement that a non-formal society of scientists and engineers has been developing in the past 30 years, who assume that all new development of information technology requires not only deductive or logical thinking - which is applicable for simple and clear tasks - but also inductive thinking. It can be described by the words "I know that I know almost nothing, but may a selection of alternative options using an external criterion open the truth". It is shown that such a thinking is very effective for the solution of complex problems of the present. In the fundamental work of Stafford Beer [1] it was shown that new knowledge cannot be obtained without effort of the outside world, without so-called external supplement. There are two ways to get such external information: The deductive approach, which is applied in the human logic, and the inductive approach that calculates an external criterion. Next to an ideal external criterion comes the LOO (leave one out) cross-validation criterion. However, in order to reduce computing time the so-called regularity criterion [2] is often used. The inductive approach, or self-organization, is used for the solution of interpolation problems of artificial intelligence, such as pattern recognition, determination of dependencies, identification of objects, or forecast of stochastic processes. The regarded book was written on a high professional level, and it can be considered as a status report of the work in this area up to the year 2000. Its forerunner [3] comparative with this scale contains information only up to the year 1985. In the preface of the book the name of the American scientist Roger Barron is mentioned who is one of the pioneers in the development of inductive algorithms. I met him on a conference on automatic control in Jerewan 1969, and since this time we have been maintaining constant scientific contacts and extremely friendly relations. He too used polynomial reference functions for the generation of model candidates. But for the estimation of the models he used internal criteria, and he tested only models that meet the rules of automatic control. Such a restriction in the selection is effective only for exact data, for which an overfitting is impossible. Among the well-known pioneers of the inductive approach to modeling certainly also ranks the author of the available book, Professor J.-A. Müller from Germany. One of its most important scientific contributions is his suggestion of the use of a Nucleus (chapter 1). The nucleus [4] is a subsample of the original data on whose basis the algorithms of self-organization generate the most accurate model. There are several algorithms known to determine a nucleus.One of it, applicable to forecast stochastic processes, can be described in the following way. First, a hierarchical clustering tree is to be developed [5]. For every clustering a first cluster can be found that contains the output vector of the sample. Then, using all first cluster of all clusterings, models are generated by self-organization. The most accurate result determines both the nucleus and the most accurate forecast. The identification of a nucleus helps increasing accuracy of the forecast of stochastic processes [6]. For pattern recognition and for the recognition of regularities, one can determine the nucleus by an analysis of columns and rows of the sample using correlation auxiliary criteria. The reduction of the original data sample, i.e., deleting less effective rows and columns, is continued as long as the external criterion is decreasing. The book is stated clear and on a good level. In it, the problem of the relation between data mining and knowledge mining appears. Further down are given some comments on this, which have only the character of advice. The book contains a preface and 8 chapters. Special attention is paid to the forecast of stochastic processes. Here, the first desire comes up: The similarity and the small difference of the algorithms for the solution of different interpolation problems should be stated in more detail. A slight modification in the form of the discrete template used during the derivation of the conditioned Gauss equations is enough to receive the system of equations for the solution of different interpolation tasks [7]. The book not only points out the achieved state in the theory of self-organization of models, but it also introduces the reader with recent problems of self-organizing modeling. A fundamental problem solved in the book is that of the relation between data mining and knowledge mining. Both deductive as well as inductive modeling is applied only in knowledge mining. An inductively driven data mining works using interpolation algorithms of artificial intelligence without application of self-organization of models. An inductively driven knowledge mining employs the same algorithms, however, with application of model self-organization. Therefore, knowledge mining results in models of large generalization power and accuracy. As follows from the book, the analysis of a sample of experimental data consists of two subsequent parts: Data mining and knowledge mining. Self-organization, i.e., the selection of alternate model variants according to an external criterion, is needed only in the second part - knowledge mining. Therefore, the book should have been better called "Self-organising Knowledge Mining" instead of "Self-organising Data Mining". Possibly, the latter title was chosen, because the book contains no algorithms for self-organization of physical models. It would be desirable to include such algorithms in a coming edition of the book. Nevertheless, the terms "self-organization of models" and "knowledge mining" are not synonymous since knowledge mining is exclusively based on the self-organization of physical models, i.e., only on the equations of dynamics. Simplified forecast models do not result in a logical interpretation, and they do not open the mechanisms of the method of operation of the object and therefore add no knowledge. An interesting fact is that at the same time with the regarded book in Novosibirsk Professor E.G. Zagorujko published his book that targets the same problems [8]. The publication of two completely independent books to the same problem underlines the worldwide topicability. One can assume that the authors of the book during the process of their writing detected the fact that all interpolation problems of artificial intelligence can be solved sufficiently exactly without modeling [6]. For example, it is enough for the pattern recognition of two alternatives to calculate the Mahalanobis-distance of the output signal to the two sample cluster. A modeling is not necessary in this case. In both books the decision if one applies knowledge mining or if limit oneself to data mining, i.e., using modeling or not, is left to the user (author of modeling). This means, this task is solved deductively. Thus, the authors deviate from the inductive approach, where the decision is made without direct participation of humans. The question whether or not it is worthwhile to apply modeling has to be solved for each variable that occurs in the sample during the process of twice self-organized networks with active neurons. This process is not sufficiently completely described in the book. All algorithms for the solution of interpolation problems contain a perceptron-type pattern [9]. They always differ from the perceptron, however, in the structure of the contained series of internal items. In the perceptron this series is not divided into cluster. The information in which cluster the largest signal will be received is lost, what from an engineering point of view is less effective. Therefore, the perceptron cannot compete with the GMDH algorithms, which have another engineer-moderate meaning. Additionally, the perceptron learns iteratively with each new line of the data sample (i.e., in the black-box regime), while algorithms of the GMDH type learn from the entire sample of the original data. Individual multi-layered neural networks considered in the book, represent perceptrons or ensembles of perceptrons that inherit all characteristics of a perceptron. From this it follows that a comparison of neural networks and self-organizing modeling, as given in the book, misses a basis. One may not compare extremely different algorithms. The book refers to nonlinear algorithms, but it not points out that all well-known work for some reason is limited to the application of in the coefficients linear polynomial reference functions. Nonlinearity is considered, but it is behind the weight coefficients that are linear. In the majority of the cases, it not came up to actually nonlinear systems. Likewise, there is no work, in which the reference functions used for the generation of the set of model candidates are selected according to an external criterion. The extrapolation of the geometrical locus of the minima of the external criterion, or the selection from a set of model candidates according to the criterion GG -> min (see below) for λ=1, gives only an approximation of the structure of the optimal physical model [7], pre-determined by the given reference function. A selection of reference functions enables the solution of the task of recognizing regularities contained in the sample of the experimental data. This important question had to be explained to the reader. It is time that we modify our relation to the iterative and genetic methods. They, as well as the perceptron, can well model the natural processes, but they are not rational for engineering problems. Regarding accuracy, they cannot compete with combinatorial algorithms, which are based on the complete selection from the set of possible model candidates. Iterative algorithms have the following lack:
The development of computer technology and the level of programming reduces the explosiveness of the computing time problem. Today, one can solve interpolation problems by means of statistical methods and discriminat analysis, i.e., on the level of data mining, very fast and accurately. Additionally, the data matrix, which must be inverted, is reduced to a bearable dimension when applying a preceding analysis of the effectiveness of its items. Self-organization of models (knowledge mining) can moderately increase accuracy in those cases only, where the data sample contains noise, for example, if some substantial variables are missing or if sufficiently many less effective variables are included in the data sample. The computing time, however, rises substantially. Therefore, it cannot be the goal of modeling to increase accuracy, but a selection of a solution that shows strong generalization power on new samples with respect to the noise level. The selection criterion is specified also. For exact data, the physical model is to be determined. The sample of an insurance company, which contains, for example, 500 variables and 20,000 customers, can be divided into two classes (a1 - prospective customers, a2 - non-prospective customers) in few minutes. The dimension of the sample is 107 items. The given function can be solved on the level of data mining using the discriminat analysis. However, in order to increase accuracy and generalization on other samples one has to move into the level of knowledge mining. At least, there is to develop a discriminat model as given, e.g., in [11] or, still better, the combinatorial GMDH algorithms has to be applied. The computing time increases to some hours. A further increase of accuracy and generalization capability can be achieved by a self-organization of some discriminat models forming a self-organized network of active neurons [12]. Note that classifying a new customer, i.e., applying the generated model, will take only a few seconds. Very often a self-organization of models can be found in those cases where the data sample contains only a part of the model arguments. This case corresponds to the presence of large additive noise. If the noise dispersion is larger than the dispersion of the output variable, a minimum of the external criterion does not exist [2]. All well-known selection algorithms do not operate. A preceding filtering of the noise can overcome that problem. It would be desirable to report on it to the reader of the book in more detail. If one considers the model as a noise filter similar to a Kalman filter [13], the question whether applying modeling or data mining, has to be decided for each variable individually. Fuzzy, very noisy variables have to go through several levels of modeling. Exact variables need no modeling. For them, one can limit to data mining. The unbiased criterion (chapter 4) would have deserved more attention. In the GMDH algorithms the optimal model is selected either according to the minimum of the external criterion of accuracy or according to the minimum of the unbiased criterion [3] or in accordance with a combined criterion GG. In the first case, the smallest error is achieved on the testing sequence B. Such a selection procedure is acceptable, if the testing sequence contains all of the figures of interest. The model error on new subsamples can become substantial, however. Using the unbiased criterion the so-called characteristic of generalization is achieved, i.e., the error on learning and testing sequence is equal. The model that corresponds to the error equality is called physical model, since it is usually easily interpretable and it describes the method of operation of the object. Intermediate solutions can be determined according to the minimum of the combined criterion GG -> min.. Here, data mining is sufficient. Apart from the accuracy of each model based on the depth of the external criterion RRB, the generalization ability of the model is of interest. For this, it is sufficient to extend the criterion for model candidates selection a little. A criterion that satisfies the demand of generalization is: whereby λ - weight coefficient of the generalization power 0 < λ < 1; RRA - minimum of the criterion of accuracy, calculated on the learning sequence; RRB - minimum of the criterion of accuracy , calculated on the testing sequence. The parameter λ is selected as a function of the completeness of the information about the data sample. So, for example, one should select λ=0 for the recognition of typeset characters, since all possible representations of the letters can be represented in the sample, and therefore the characteristic of generalization is not required. When recognizing handwritten letters, in contrast, only a part of the representations is contained in a sample and the generalization capability of the model is necessary. Here, one selects now λ=1, i.e., it is used a physical model. Additionally, the weight coefficient λ is selected with consideration of the information about the conditions of work of the model. If the arguments of the model and the variables of the output sample have an equal noise dispersion, λ=0 is selected. Here, a non-physical model is obtained for clustering or forecasting. If exact data is used then one selects λ=1. In this case the criterion is named unbiased criterion [3] and the resulting model is called physical model. For complex models the internal criterion RRA will decrease with increasing complexity of the model while the external criterion RRB will grow. The intersection determines the structure of the physical model by the given reference function (fig. 1). 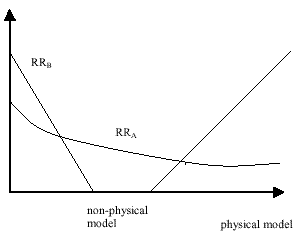
Figure 1: Self-organization of a physical model using inductive selection procedures The questions discussed in the chapters 5 and 6 are very important for the theory of self-organization of models. They are so interesting that they appear suitable as topics for new independent books. In chapter 5, algorithms of self-organization of models with fuzzy input variables are described. Important is to note that the fuzzy character of the variables can be even more complex, up to the consideration of a type of psychological variables, which cannot be submitted a measurement or a formalization at all. Such a consideration becomes possible with the help of a parametric noise filtering using algorithms of self-organization of models. It is shown that these algorithms possess characteristics of the Kalman noise filters. Also in chapter 5 the use of analogs is suggested for the solution of interpolation problems in place of models. A completing description of neural networks with active neurons would be desirable, whereby these analogs are used as active neurons [14]. Likewise, it should be paid more attention on the generation of secondary arguments (characteristics) and their estimation on the information level by auxiliary functions of the correlation type. Finally, I'd like to say that the book does not only inform the reader about the level of development of the theory of self-organization of models, but it also refers to questions of generalization of models on new data samples. This problem is only at the start of its solution. Many further problems of self-organization of models are solved yet, and they are reported in detail in the regarded book.
|

